Isaksen, Leif, University of Southampton, UK, leifuss@googlemail.com
The Geographike hyphegesis of Claudius Ptolemy (c. 90-c. 168 CE) – more commonly known as the ‘Geography’ but hereafter referred to as GH – is perhaps the most important text in the history of digital cartography. While its fame derives from the enormous catalogue of ancient places that have made it indispensable for those studying ancient geography, its central innovations of presenting locations as tables of coordinates and offering multiple projections by which to represent them make it the foundational work for all modern Geographic Information Systems (GIS). Yet despite this historic legacy it remains a deeply problematic text (Dilke 1987). The sheer quantity, breadth and apparent precision of the catalogue greatly surpass that of every other known work of ancient geography. How did a lone scholar, working with only published materials, compile such a comprehensive overview of the inhabited world (oikumene)? And what provoked his revolutionary shift in methodology?
Several research projects have used digital methods to examine aspects of Ptolemy’s Geography in recent years. Most significant is Stückelberger and Graßhoff’s database of coordinates (2006) which forms the baseline data for the research presented. Despite creating this excellent resource, their analysis (Stückelberger & Mittenhuber 2009) remains a fairly traditional close reading of the text, makes scant explicit use of the digital data. Tsorlini (2009) used digital methods to show coordinate discrepancies between different manuscripts, although these largely focus on the medieval maps, the provenance of which remains unclear (Mittenhuber 2010). Kleineberg et al. used digital transformations in order to ‘georectify’ the coordinates in the region of Germania Magna and thus propose the identification of many hitherto unidentified locations with modern sites (2010).
Conventional wisdom is that GH is the culmination of a long tradition of Greek geographical and astronomical science, augmented and improved at each stage by contemporary sources such as merchant’s reports, itineraries and astronomical observations (Berggren & Jones 2000: 25-30). This paper will present several arguments based on digital methods to demonstrate that this view is almost certainly wrong and that Ptolemy’s treatise is a highly original work that fuses two distinct traditions for a specific purpose: the calculation of local celestial and solar phenomena for astrological prognostication. This goal required the combined data of Greek geographic maps – which represented the inhabited world schematically but in relation to cosmological constants such as the poles and equator – and Roman chorographic maps, which represented the world in a series of densely populated but geospatially unanchored regional images. It was the challenge of bringing together these very different traditions which led Ptolemy to apply the data management techniques he had used for astronomical data in the Almagest and thus the lay the groundwork for late medieval geography and ultimately the GIS systems of today.
While Digital Humanities is not the forum to lay out a full argument for Ptolemy’s motives and the nature of his sources – which will be expressed in a forthcoming paper – the following preliminary points should be made. First, his astrological ambitions are no surprise. Ptolemy’s Tetrabiblos became the principle work on the topic for almost a millennium and he explicitly refers to the practice of calculating celestial phenomena for terrestrial locations in the Almagest (2.3; 8.6), GH itself (1.1; 8.2) and the Manual to the Handy Tables. No other practical motive is given for GH’s construction and thus there is no reason to believe that it was ever intended for an alternative purpose. The second point is that while we have virtually no extant examples of pre-Ptolemaic geographic or chorographic maps, the written sources – including Ptolemy’s distinction between the two practices in GH (1.1) – offer some important clues. The mathematical precision of geographia is explicitly stated by Ptolemy, but evidence as to the paucity of its content can be adduced from fragments of the three authors most likely to have been sources to Ptolemy – Eratosthenes, Hipparchus and Marinos of Tyre. Ignoring those on the Persian Royal Road, the places they mention are overwhelmingly (~90%) located on coastlines and boundaries. This is stark contrast to GH in which interior locations outnumber liminal ones by about 3:2. In contrast, both Ptolemy and Strabo (Geog. 2.5.17) refer to the richness of chorographic content but a strong indication of their unsuitability for astrology is given by the absence of any geodetic information for the Agrippan ‘World Map’ and other chorographic sources.
Statistical distributions of precision
Ptolemy’s coordinates are expressed as fractions of a degree of latitude (measured from the equator) and longitude (measured from an arbitrarily defined prime meridian in the Atlantic ocean). Superficial examination makes clear that the smallest latitudinal and longitudinal increment is 1/12 of a degree (or 5 minutes) of arc. As real world locations are themselves distributed randomly, we would expect a relatively even distribution of Ptolemaic locations with respect to the fraction of degree upon which they fall. In fact their distribution is highly uneven (Figure 1), a phenomenon also observed by Marx (2011). We know that some locations (which we shall refer to as ‘high precision’ locations) must have been assigned to the nearest twelfth of a degree, as they fall on divisions that are indivisible by lower denominators.1 However, the uneven distribution makes it clear that significantly more of the coordinates are assigned at lower levels of precision: sometimes just to the nearest degree. The challenge is to establish which of them have been plotted more or less precisely. While it is not possible to do this by considering each location individually the fact that Ptolemy’s principles are so closely aligned with GIS make it an ideal tool for investigating the data’s underlying structure.
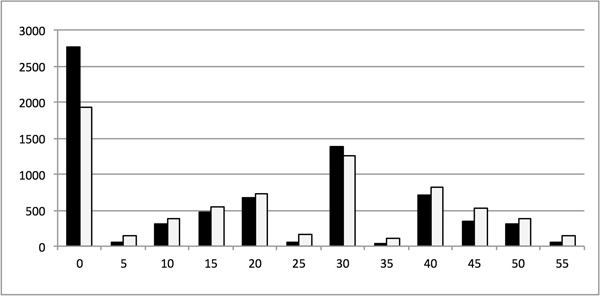 Figure 1: Quantity of coordinates falling on latitudinal (white) and longitudinal (black) degree divisions (in minutes)
Figure 1: Quantity of coordinates falling on latitudinal (white) and longitudinal (black) degree divisions (in minutes)
Spatial distribution of precision
The first clues as to the spatial distribution of ‘high precision’ locations emerge from plotting all locations which are definitely assigned to the nearest twelfth of a degree in a GIS2 (Figure 2). This demonstrates beyond all doubt that a core body of data – comprising Hispania, Italia and its major island neighbours, Greece, Asia Minor, the Levant and Egypt – contains virtually all known coordinates assigned to this high level of precision. The phenomenon appears in both manuscript traditions. In contrast, the peripheral regions, which include such well-established roman regions as Gaul and Africa Proconsularis, are almost entirely devoid of ‘high precision’ locations. Furthermore, although latitude is generally more likely to be of high precision than longitude, this is not caused by the well-known ‘Problem of longitude’ (Sobel 1995). Latitude can be hopelessly incorrect in some ‘high precision’ regions (such as Sardinia) so it is evident that these values have not been determined from empirical measurements.
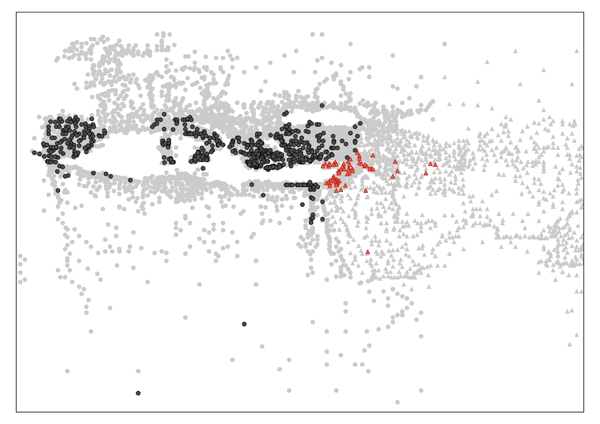 Figure 2: Coordinates know to be assigned at a precision of 1/12 of a degree of latitude or longitude. The effect is observed in both Ξ (black) and Ω (red) recensionsFigure 2: Coordinates know to be assigned at a precision of 1/12 of a degree of latitude or longitude. The effect is observed in both Ξ (black) and Ω (red) recensions
Figure 2: Coordinates know to be assigned at a precision of 1/12 of a degree of latitude or longitude. The effect is observed in both Ξ (black) and Ω (red) recensionsFigure 2: Coordinates know to be assigned at a precision of 1/12 of a degree of latitude or longitude. The effect is observed in both Ξ (black) and Ω (red) recensions
Linear interpolation
The order in which Ptolemy’s coordinates are listed is not random. The description of each region follows a strict sequence commencing with boundaries, followed by physical geography, continuing with inland cities and concluding with offshore islands. The boundaries and physical features are typically linear in form and so topographically adjacent locations are listed consecutively to facilitate the drawing of lines or iconography between them. Islands are also listed in the sequence in which they follow a coastline wherever possible. Much more interesting for this analysis are the cities of the interior, for there is no natural order for Ptolemy to follow and so they may betray information as to the manner in which they were obtained.
We can visualize this order very easily by simply ‘joining the dots’ in sequence and colour coding the individual regions. Once again, the results display a striking disparity between the core regions and the periphery. In the core data, coordinates group together in tightly bunched clusters. At the periphery they are generally ‘sketched out’ in linear zig-zagging rows, usually horizontally (Europe, much of Asia) or vertically (Africa), but occasionally in a NE-SW sweep (India). A comparison with the ‘high precision’ coordinates over these features clearly demonstrates a correlation between this stylistic variation and the ‘core’ data we identified previously (Figure 3).
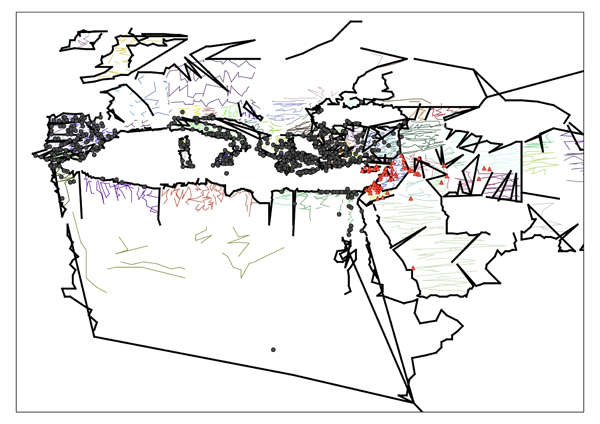 Figure 3: Detail showing lines interpolated between settlements overlaid with ’high precision’ coordinates
Figure 3: Detail showing lines interpolated between settlements overlaid with ’high precision’ coordinates
Two Coordinate Systems
We can push this further. Despite the apparent regularity of Ptolemy’s 180 x 360 coordinate grid (first developed by Hipparchus (Dicks 1960: 32-33)), he also makes reference to a traditional series of irregular Greek parallels (based on the length of the longest day) and tripartite divisions of the ‘hour intervals’ – the ‘time-zones’ of antiquity. So which coordinate system is Ptolemy using? The answer is most clearly illustrated by examining Ptolemy’s regional map of Arabia Felix and Karmania. Ptolemy lists a series of tribal and geographic divisions along the coast of the Arabian peninsula and it is apparent that their locations are defined with reference to the traditional coordinate system (Figure 4). Yet the interior, which contains no differentiation and is simply a list of towns conforms, to the entirely separate Hipparchan framework (Figure 5).
We must be careful to jump to conclusions too readily for, as we have seen, there is much regional variation in Ptolemy’s sources, but a consistent pattern emerges in both core and periphery. Boundaries make reference to the coarse-grained and irregular, traditional Greek framework whereas internal cities generally conform to the fine-grained and regular coordinate system. Returning to our earlier argument, there is an obvious explanation. Ptolemy’s goals required him to use Greek geographic maps as a framework if he was to compare terrestrial and celestial locations. Yet we know that the data they provide is scanty. His solution was to peg chorographic maps to this global framework, thereby eliminating systemic error at the cost of local accuracy.
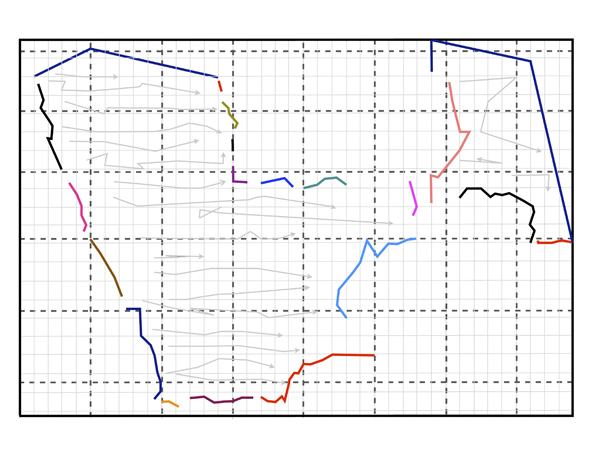 Figure 4: Ptolemy’s map of Arabia Felix and Karmania showing how tribal divisions and structure are associated with traditional Greek parallels and divisions of ‘hour intervals’
Figure 4: Ptolemy’s map of Arabia Felix and Karmania showing how tribal divisions and structure are associated with traditional Greek parallels and divisions of ‘hour intervals’
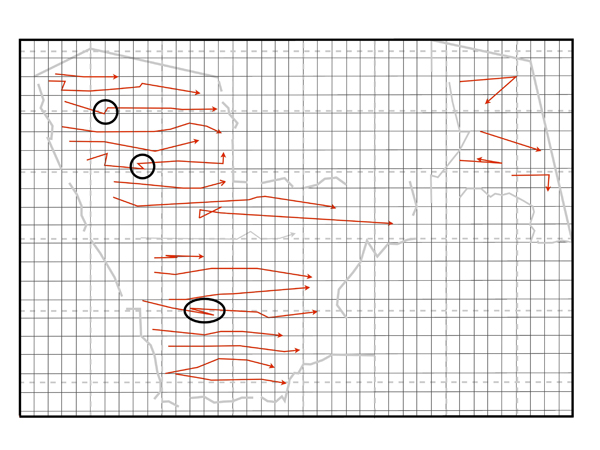 Figure 5: Ptolemy’s map of Arabia Felix and Karmania showing how the order of undifferentiated cities of the interior is influenced by the Hipparchan coordinate system
Figure 5: Ptolemy’s map of Arabia Felix and Karmania showing how the order of undifferentiated cities of the interior is influenced by the Hipparchan coordinate system
References
Berggren, J. L., and A. Jones (2000). Ptolemy’s Geography. An Anntoated Translation of the Theoretical Chapters. Princeton: Princeton UP.
Dicks, D. R. (1960). The Geographical Fragments of Hipparchus. London: Athlone Press.
Dilke, O. A. W. (1987). The Culmination of Greek Cartography in Ptolemy. In J. B. Harly and D. Woodward (eds.), The History of Cartography. Chicago: U of Chicago P, vol. 1, pp. 177-200.
Kleineberg, A., et al. (2010). Germania und die Insel Thule. Darmstadt: Wissenschaftliche Buchgesellschaft.
Marx, C. (2011). On the precision of Ptolemy’s geographic coordinates in his Geographike Hyphegesis. History of Geo- and Space Sciences 2(1): 29-37.
Mercier, R. (2011). Ptolemaiou Procheiroi Kanones. Ptolemy’s Handy Tables. Leuven: Peeters.
Sobel, D. (1995). Longitude. The True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time. London: Fourth Estate.
Jones, H. L. (1917). The Georgraphy of Strabo. London: Heinemann, vol. 1.
Stückelberger, A., and G. Graßhoff (2006). Ptolemaios. Handbuch der Geographie. Basel: Schwabe.
Stückelberger, A., and F. Mittenhuber (2009). Ptolemaios. Handbuch der Geographie. Ergänzungsband. Basel: Schwabe.
Toomer, G. J. (1984). Ptolemy’s Almagest, London: Duckworth.
Tsorlini, A. (2009). Higher Order Systematic Effect in Ptolemy’s Geographia Coordinate Description of Iberia. e-Perimetron 4(2): 117-130.
Notes
1.At 5 minutes (1/12), 25 minutes (5/12), 35 minutes (7/12) and 55 minutes (11/12)
2.Those that fall on the traditional 2nd, 4th, 11th, 12th, 13th, anti-2nd and anti-4th Greek parallels (which also happen to be ‘high precision’ for arbitrary reasons) have also been removed here for reasons which will become clear.

